C 問題についてのみ書きます。

Hello 2020 C New Year and Permutation

問題

順列$p_1, p_2, …, p_n$が与えられる。このとき、部分列$[l,r]$であって$max(p_l,…,p_r) - min(p_l,…,p_r) = r - l$が成り立つものを framed segment と呼ぶことにする。すべての長さ$N$の順列に対して、framed segment の数を数え上げてその和を素数$M$で割った値を求めよ。

解法

順列が与えられて、それに対する framed segment の数を数えると$O(N!)$になってしまい計算量的に無理。そこで、視点を変えてサイズ$k$の framed segment を横断的に数え上げる方法を考える。
サイズ$k$の framed segment の位置、内部で使われる数の集合(順番は無視する)を考える。

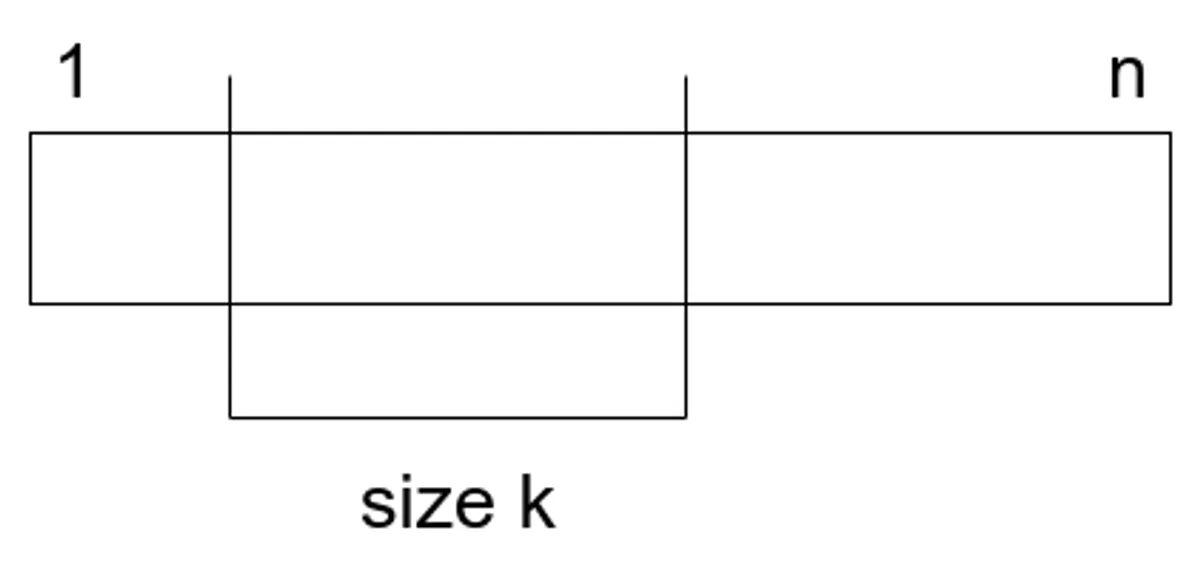
図のように位置はスタート地点が$1$から$n-k+1$で全部で$n-k+1$通りある。
また、内部で使われる数は、$r-l+1$個の相異なる数の最大値と最小値の差が$r-l$であることから、連続した$k$個の数なので、これもスライドして考えると$n-k+1$種類ある。

次に、framed segment 外部と内部の順列を考える。これは、内部で$k!$通り、外部で$(n-k)!$通りである。

$1 \leq k \leq n$よりこれらを足し合わせて$m$で割れば答えが得られる。

実装

最後の足し合わせるところで$O(N)$であるので、$N \leq 250000$から各 framed segment のサイズごとは$O(\log N)$以下の計算量である必要がある。
ここで、factorial は$f(n) = f(n-1) \times n$であることを考えると、これは配列と非常に相性がよく、前計算をしてその配列を使えばよいとわかる。

vector<i64> fact(n+1);
fact[0] = 1;
for(i64 i=1;i<=n;i++)fact[i] = fact[i-1]*i%m;
for (k=1;k<=n;k++){
    res += (サイズkのframed segmentの数)
}

注意としては、サイズ k の framed segment の数を求める時の overflow である。一つ掛けるごとに MOD をとらなければ違う答えになってしまった。
計算量は前計算$O(N)$, res に足し合わせて$O(N)$で全体で$O(N)$である。

コード

https://codeforces.com/contest/1284/submission/68567949

感想

はじめは MOD が関わるライブラリゲーだと思って mod_factorial なる関数を作ったが意味なかった。でもまた同じ思考になるかもしれないので、ライブラリのコメント欄に書いておいた。
ModInt 理解したい。